Euler's formula:
Introduction: Beauty
The author discusses the meaning of "exquisite beauty." It almost comes down to: "I can't define beauty, but I know it when I see it." And Euler's identity is "beautiful." I, for one, have always been intrigued by that identity. I don't recall seeing it while in college, but came across it only in the last ten years or so.
Chapter 1: Complex Numbers
This might be the longest chapter. I haven't finished the book yet, nor have I looked at the Table of Contents, so I don't know, but it is a long chapter. Unlike Euler's identity, I have known about complex numbers and imaginary numbers since high school, I assume, but certainly since college, I hope. But like Euler's identity, complex numbers and imaginary numbers have always fascinated me. I doubt anyone can really visualize the "square room of -1," but my nephew, an engineer working on electronic systems for wide-body jets (US and European) laughs when he says how often imaginary numbers show up in his work. It seems it should be unnerving to the flying public if they knew that the math behind modern jets is based on imaginary numbers (of course, airline profits, it seems are also based on imaginary numbers, so perhaps it all evens out in the end).
The author used Euler's formula to explain complex numbers. Or maybe he uses complex numbers to explain Euler's formula. I need to re-read this chapter, later, and more slowly.
Chapter 2: Vector Trips
The author uses Euler's formula to explain that a wind actually increases the round trip time for a bird flying with / against the wind in a perfectly symmetrical fashion (equal distance both ways; equal wind both ways).
By the way, the same problem/solution demonstrates that the sports world practice of not allowing records to be recognized if the wind is too strong makes no sense for races that require an integral number of closed loops around a track (of any shape). "Indeed, if a record is set in such an event with a constant wind blowing in any direction, then the record should absolutely count because the athlete would have done even better without the wind."
The author also explains the "cat-and-mouse-pursuit problem" using the same formula.
Chapter 3: The Irrationality of pi-squared (π2)
The author discussed how Euler's formula proves the irrationality of pi-squared (π2). The author begins with a bit of philosophy cited from another source:
"Does it really matter that π (pi) is an irrational number? Do physicists or engineers really need to know the value of π beyond, say 3.13159265 (or even the crude approximation that schoolchildren are often taught, 22/7). Probably not: it is now accepted among plumbers, a fact impressed on all apprentices, that the circumference of a pipe is found by multiplying the diameter by π ... I am of course perfectly well aware of the irrationality of π, but, on the job, π is 3 1/7, or 3 if I am in a hurry."Chapter 4: Fourier Series
Chapter 5: Fourier Integrals
Chapter 6: Electronics and √−1
Euler: The Man and the Mathematical Physicist
.... there is still not even one book-length biography, in English, of Euler ... Euler himself wrote so prodigiously that it would be a huge undertaking for a biographer to write, with true understanding, of what he actually did. Euler wrote, you see, more than any other mathematician in history. During his lifetime more than five hundred (!) books and articles by him were published (even more after his death), and his total work output accounts for a third of all that was published in Europe on mathematics, theoretical physics, and engineering mechanics from 1726 to 1800. In addition, there is another, equally enormous body of surviving personal letters (nearly 3,000 of them to and from hundreds of individuals), more thousands of pages of research notebooks, and voluminous diary entries that he continuously generated from his college days until his death. A dedicated biographer will have to read it all.
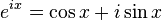
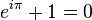
No comments:
Post a Comment